Power Factor

A look at how power factor influences electric meter testing

(You can listen to this blogpost too!)

In our first blog post of the fundamentals series, we discussed the basics of voltage and current.  This post discusses the concept of power factor and power, and why they are important to meter testing.

Power is the result of current and voltage applied to some form of load.  It is representative of the amount of work the load does.  Voltage
by itself doesn’t do much.  It only has value when it is applied to a load, which can be anything from a light, a motor, or a complex industrial system.  The standard value of power is called a Watt.  One Watt is the amount of work that occurs when one Volt and one Amp are applied to a load.  Hence the basic formula, P=I*V, or Power (in Watts) = Voltage (in Volts) times Current (in Amps).

Previously we expressed load simply as being a resistor or something small.  In metering, when the word load is used, it refers to the entire facility that is being metered at a certain point.  All the lights, the computers, the motors, the air conditioners, or any other device using electricity is considered part of the load.  Before we proceed, let’s look at some different values that are commonly used in reference to load.

Resistive Load:  This is the common load everybody learns about.  Most commonly thought of as a resistor, it allows current to flow through it.

Inductive Load:  This type of load is extremely common in the world (e.g. motors), and is based off inductors.  Inductors oppose change in current, and cause the current waveform to lag behind the voltage waveform.

Capacitive Load: Rare in typical loads, capacitors resist changes in voltage, and causes the current to lead the voltage.

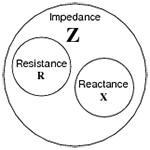Impedance: Your new form of resistance!  A combination of resistance and reactance (made up of inductance and capacitance).

There is no real need to go into the calculations or too much detail about what makes up the load except to understand the type of loads out there affect the power in many ways.  So much that there are actually three terms for power.

• Watts — Actual amount of power dissipated in a circuit.  Also called:
  1. Real Power
  2. True Power
  3. P
  4. Can be positive or negative
• Volt-Amps — Product of a circuit’s voltage and current, without reference to phase angle.  Also called:
  1. Apparent Power
  2. S
  3. Always an unsigned value, neither positive or negative
• Volt-Amps Reactive — Power absorbed and returned in loads due to reactive power.  Also called:
  1. Vars
  2. Reactive power
  3. Q
  4. Can be positive or negative.

The lower the Power Factor gets, the less efficient the load is from a power generation standpoint.

Three powers?  What’s the difference?  How do I remember or keep track of all these powers and what they do?  Think back two paragraphs to the terms inductive load and capacitive load.  Remember that these resist change in current and voltage, respectively.  When this happens, the current and voltage are no longer in phase with each other, resulting in a loss of work.  The closer the voltage and current waveforms are to each other, or the more in phase they are, the more efficiently the system is consuming available power.  In fact, there is a quantity or term that indicates the “efficiency” of a load, and it is called the Power Factor.  A system’s Power Factor is a value from -1 to 1 that indicates the phase relationship between the voltage and current.  A Power Factor of 1, also known as unity, indicates the load is acting as a purely resistive load.  The lower the Power Factor gets, the less efficient the load is from a power generation standpoint.

As mentioned earlier, a loads impedance is a combination of the resistance along with the reactance.  Reactance is either the load’s inductance or capacitance.  A purely resistive load has no phase shift between the voltage and the current.  Remember the following phrase, “ELI the ICE man”, which describes the following terms and their relationships:

E – Electromotive force, Voltage

I – Current

C – Capacitance

L – Inductance

ELI represents that in an inductive circuit, the current is lagging the voltage (E comes before I).  ICE gives the current leading the voltage in a capacitive circuit (I comes before E).  These reactive loads are what determines the phase shift between the voltage and current, which is where we get the Power Factor.

How does this affect metering, billing and other aspects?  For that, we turn back to our power definitions.  Watts is called real power, or the amount of power being used to perform the load.  A unity Power Factor indicates the load is utilizing all the power available to it.  A non-unity Power Factor reduces the amount of Watts being used.  But that’s good right?  No, in fact it is the opposite of good.  VA, or Volt-Amps is the amount of power that the utility company has to provide to compensate for the load.  It is the apparent power, or the total power available that is being used.  VARs or Volt Amp’s Reactive, is the amount of power stored due to inductance and capacitance.

Imagine a tall glass filled with water.  This is a system with a unity Power Factor.  The glass is the VA, or the amount of power required, the water is the real power being used.  When the glass is less than full, it is not as efficient as a full glass of water for quenching ones thirst.

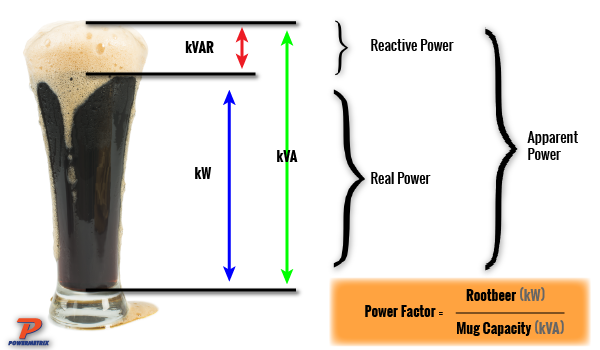
Now, imagine that same glass and somebody pours root beer in it.  As we know, root beer is frothy and foamy.  The glass still represents the amount of power provided, the liquid is the Watts, the power being used, and the frothy part at the top that takes up space is the VARs, serving no purpose except keeping the glass from being fully utilized with delicious root beer.

To cap it all off, understanding the way voltage and current interact with the load is vital to understanding the metering aspects of a site.  When the voltage and current are applied to a load, which has an impedance, the current waveform will either stay in phase with, or shift out of phase with, the voltage.  A unity Power Factor is ideal, it’s a full glass of cool root beer. No VARs are present, and the VA and Watts are equal.  Non-unity Power Factor gives us the appearance of a full cup, but in reality the VARs are wasted foam, and we can only utilize a portion of the cup’s capacity to drink our root beer in.

We love hearing from you!  If you’ve got a question or comment, leave it below.